Non-empirical, low-cost recovery of exact conditions with model-Hamiltonian inspired expressions in jmDFT

Abstract

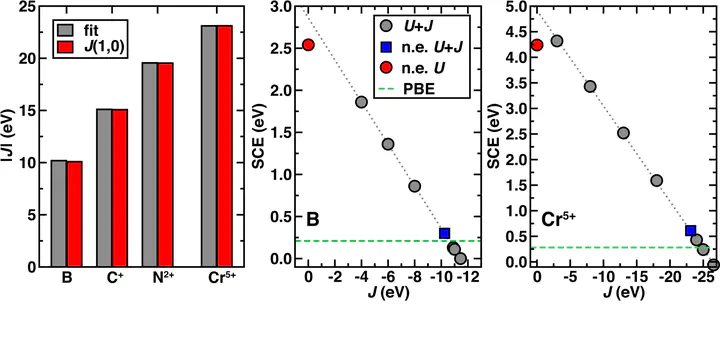
Density functional theory (DFT) is widely applied to both molecules and materials, but well known energetic delocalization and static correlation errors in practical exchange-correlation approximations limit quantitative accuracy. Common methods that correct energetic delocalization errors, such as the Hubbard U correction in DFT+U or Hartree-Fock exchange in global hybrids, do so at the cost of worsening static correlation errors. We recently introduced an alternate approach [Bajaj et al., J. Chem. Phys. 147, 191101 (2017)] known as judiciously modified DFT (jmDFT), wherein the deviation from exact behavior of semilocal functionals over both fractional spin and charge, i.e., the so-called flat plane, was used to motivate functional forms of second order analytic corrections. In this work, we introduce fully nonempirical expressions for all four coefficients in a DFT+U+J-inspired form of jmDFT, where all coefficients are obtained only from energies and eigenvalues of the integer-electron systems. We show good agreement for U and J coefficients obtained nonempirically as compared with the results of numerical fitting in a jmDFT U+J/J′ correction. Incorporating the fully nonempirical jmDFT correction reduces and even eliminates the fractional spin error at the same time as eliminating the energetic delocalization error. We show that this approach extends beyond s-electron systems to higher angular momentum cases including p- and d-electrons. Finally, we diagnose some shortcomings of the current jmDFT approach that limit its ability to improve upon DFT results for cases such as weakly bound anions due to poor underlying semilocal functional behavior.