Abstract
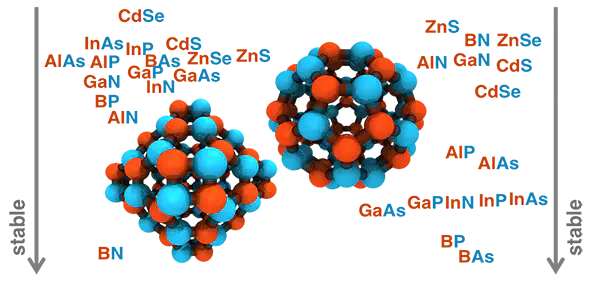
We present a systematic, first-principles study of the role of elemental identity in determining electronic, energetic, and geometric properties of representative A28B28, A30B30, and A36B36 III–V (A = B, Al, Ga, or In and B = N, P, or As) and II–VI (A = Zn or Cd and B = S or Se) fullerene allotropes. A simple descriptor comprising electronegativity differences and covalent radii captures the relative fullerene stability with respect to a nanoparticle reference, and we demonstrate transferability to group IV A72 (A = C, Si, or Ge) fullerenes. We identify the source of relative stability of the four- and six-membered-ring-containing A36B36 and A28B28 fullerene allotropes to the less stable, five-membered-ring-containing A30B30 allotrope. Relative energies of hydrogen-passivated single ring models explain why the even-membered ring structures are typically more stable than the A30B30 fullerene, despite analogies to the well-known C60 allotrope. The ring strain penalty in the four-membered ring is comparable to or smaller than the nonpolar bond penalty in five-membered rings for some materials, and, more importantly, five-membered rings are more numerous in A30B30 than four-membered rings in A36B36 or A28B28 allotropes. Overall, we demonstrate a path forward for predicting the relative stability of fullerene allotropes and isomers of arbitrary shape, size, and elemental composition.