Predicting transition forces using the tensioned model for bond activation (TMBA)
We developed the tensioned model for bond activation (TMBA), a multivariate linear regression model trained on experimentally studied covalent mechanophores that can accurately predict transition forces in polymer mechanochemistry. In this tutorial, we will show how to calculate the transition force ($f^*$) using TMBA.
TMBA facilitates high-throughput virtual screening of diverse mechanophores. You can read about the model in more detail here.
All input files, output files, and scripts can be downloaded from a link at the end of the tutorial. Today’s example for calculating activation force is cis-acyl-NEO, a mechanophore based on a neobornenone scaffold that can release CO under tension:
The use of the TMBA requires the calculation of two parameters: the effective force constant ($k_{\rm eff}$) and the force-free reaction energy ($\Delta E$).
Calculating the effective force constant
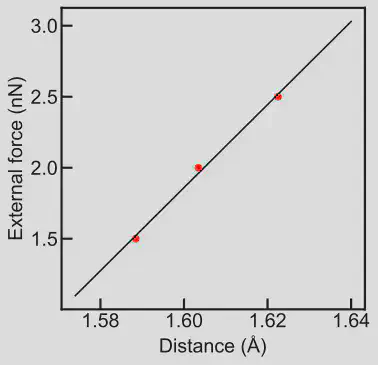
The effective force constant calculation requires optimized structures of the reactant under tension, and can be performed using the slope of the external applied force as a function of bond distance of the cleaving bond (in our example, atoms 16 and 21). Here, we will optimize the structure of cis-acyl-NEO under three distinct applied forces, where the force is applied to two terminal methyl groups (atoms 20 and 25).
The input file for optimizing a structure under tension using the ORCA software package looks like the following:
! B3LYP D3BJ Opt def2-svp RIJCOSX
%pal nprocs 8 end
%geom POTENTIALS
{C 20 25 1.5}
end
end
* xyzfile 0 1 cis-acyl-neo.xyz
After the optimizations are completed, we obtain cleaving bond distances at three different external applied forces. In this example, these values were found to be 1.588, 1.603, and 1.622. Using a linear fit, we obtain a value of $k_{\rm eff}$ of 29.2.
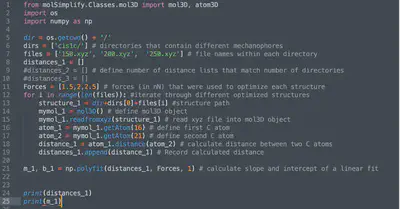
The distances can be obtained by either manually inspecting bond distances with molecular visualization software or by using the custom Python script provided below (calc_keff.py), which uses the molSimplify software package.
Calculating the force-free reaction energy
The force-free reaction energy ($\Delta E$) can be calculated by optimizing the reactant and the diradical intermediate separately, followed by single-point calculations using a larger basis set. An input file for ground state optimization is provided below:
! B3LYP D3BJ Opt def2-svp RIJCOSX
%pal nprocs 8 end
* xyzfile 0 1 cis-acyl-neo.xyz
The optimization of a diradical intermediate can be achieved through broken symmetry DFT (BS-DFT), however this can be complicated due to the geometry convergence to a closed-shell structure. This can be avoided by obtaining a triplet geometry instead, which can serve as an approximate singlet diradical structure. Job inputs for optimizing both ground state singlet diradical and triplet intermediate structures are provided below, and singlet diradical optimization should be attempted first. In case of failure, triplet geometry can be used as a substitute:
Singlet diradical:
! uks B3LYP D3BJ Opt def2-svp RIJCOSX
%pal nprocs 8 end
%scf
Brokensym 1,1
end
* xyzfile 0 1 intermediate.xyz
Triplet:
! B3LYP D3BJ Opt def2-svp RIJCOSX
%pal nprocs 8 end
* xyzfile 0 3 cis-acyl-neo.xyz
Finally, we carry out a single-point calculation using a larger basis set. The job inputs for single-point calculation for ground state and diradical intermediates are provided below:
Ground state:
! uks b3lyp d3bj def2-tzvpp RIJCOSX
%pal nprocs 8 end
* xyzfile 0 1 reagent.xyz
Diradical:
! uks b3lyp d3bj def2-tzvpp RIJCOSX
%pal nprocs 8 end
%scf
Brokensym 1,1
end
* xyzfile 0 1 intermediate.xyz
Using this approach, we obtain the force-free reaction energy of 59.4 kcal/mol.
Generating a prediction from TMBA
In our recent work, the TMBA model was parametrized against experimental mechanochemical data. The resulting formula for the transition force in terms of the effectice force constant and the force-free reaction energy was found to be: $f^* = 0.0237\times\Delta E + 0.0494\times k_{\rm eff} - 0.495$
Plugging in the computed parameters we obtain: $f^* = 0.0237\times59.4 + 0.0494\times 29.2 - 0.495 = 2.36 {\rm \ nN}$, which is in good agreement with the experimentally measured transition force of 2.51 nN.
Here, we have provided a brief walkthrough on using TMBA to predict the transition forces of covalent mechanophores. We hope you found this tutorial helpful and can use this approach for the accelerated screening of mechanophores!
Scripts and Files:
