DFT-based Multireference Diagnostics in the Solid State: Application to Metal-organic Frameworks

Abstract

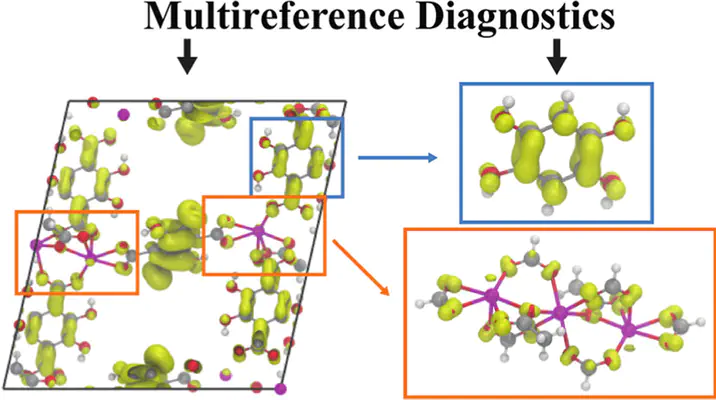
When a many-body wave function of a system deviates far from a single reference determinant, high-level multireference methods are required to properly explain the system. Multireference diagnostics to estimate the magnitude of such static correlation have been primarily developed for molecular systems, with a range of computational costs from low to as costly as the full multi-reference calculation itself. We report the first application of low-cost multireference diagnostics on the solid state based on the fractional occupation number calculated with finite-temperature density functional theory (DFT). In order to compare the behavior of the diagnostics on solids and molecules, we select metal-organic frameworks (MOFs) as model materials, since their reticular nature provides an intuitive way of identifying molecular derivatives. Two possible molecular fragmentations are considered: 1) breaking it down into its substituent secondary building unit and linker components and 2) extracting it in a finite cluster with a single metal atom. We demonstrate that the DFT-based multireference diagnostics are equally applicable to solids as to molecules. The magnitude and spatial distribution of the multireference character of a MOF are found to have a good correlation with those of the molecular derivatives, which can be calculated much more affordably in comparison to the full MOF. The additivity feature of the multireference character discussed here suggests molecular derivatives as a good representation of a MOF, facilitating accurate and efficient high throughput screening of MOFs and other porous solids.