Ligand-Field-Dependent Behavior of Meta-GGA Exchange in Transition-Metal Complex Spin-State Ordering
Abstract
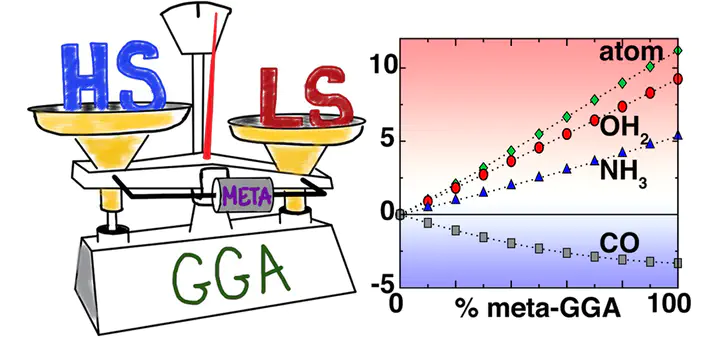
Prediction of spin-state ordering in transition metal complexes is essential for understanding catalytic activity and designing functional materials. Semilocal approximations in density functional theory, such as the generalized-gradient approximation (GGA), suffer from several errors including delocalization error that give rise to systematic bias for more covalently bound low-spin electronic states. Incorporation of exact exchange is known to counteract this bias, instead favoring high-spin states, in a manner that has recently been identified to be strongly ligand-field dependent. In this work, we introduce a tuning strategy to identify the effect of incorporating the Laplacian of the density (i.e., a meta-GGA) in exchange on spin-state ordering. We employ a diverse test set of M(II) and M(III) first-row transition metal ions from Ti to Cu as well as octahedral complexes of these ions with ligands of increasing field strength (i.e., H2O, NH3, and CO). We show that the sensitivity of spin-state ordering to meta-GGA exchange is highly ligand-field dependent, stabilizing high-spin states in strong-field (i.e., CO) cases and stabilizing low-spin states in weak-field (i.e., H2O, NH3, and isolated ions) cases. This diverging behavior leads to generally improved treatment of isolated ions and strong field complexes over a standard GGA but worsened treatment for the hexa-aqua or hexa-ammine complexes. These observations highlight the sensitivity of functional performance to subtle changes in chemical bonding.