Ligand Additivity and Divergent Trends in Two Types of Delocalization Errors from Approximate Density Functional Theory

Abstract

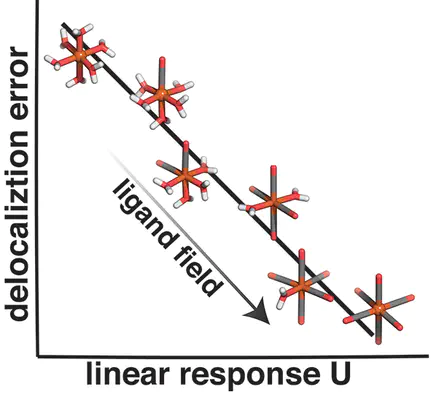
The predictive accuracy of density functional theory (DFT) is hampered by delocalization errors, especially for correlated systems such as transition-metal complexes. Two complementary strategies have been developed to reduce delocalization error: eliminating the global curvature with change in charge and computing a linear response Hubbard U as a measure of local curvature at the metal center at fixed charge and applying it to the transition-metal complex in a DFT+U framework. We investigate the relationship between the two delocalization error measures as the ligand field strength is varied with the number of strong-field ligands in a series of heteroleptic complexes or by geometrically constraining the metal–ligand bond length in homoleptic octahedral complexes. We show that across these sets of complexes an inverse relationship generally exists between global and local curvatures. We find that effects of ligand substitution on both measures of delocalization are typically additive, but the quantities seldom coincide.